最近在刷LeetCode，剛好科普一下「時間複雜度（Time Complexity）」與「空間複雜度（Space Complexity）」。

在軟體開發和演算法設計中，我們經常需要評估演算法的效率。其中，「時間複雜度」和「空間複雜度」是兩個關鍵概念，對於評估算法性能至關重要。本篇技術分享將淺顯易懂地介紹這兩個概念，並以Python為例進行示範。

時間複雜度 Time Complexity

簡單的來說就是，電腦執行演算法所需要耗費的時間成本。

時間複雜度描述了一個算法執行所需的時間，通常以「步驟數」表示。這裡的「步驟」可以指基本操作的次數，或者是其他衡量執行效率的單位。

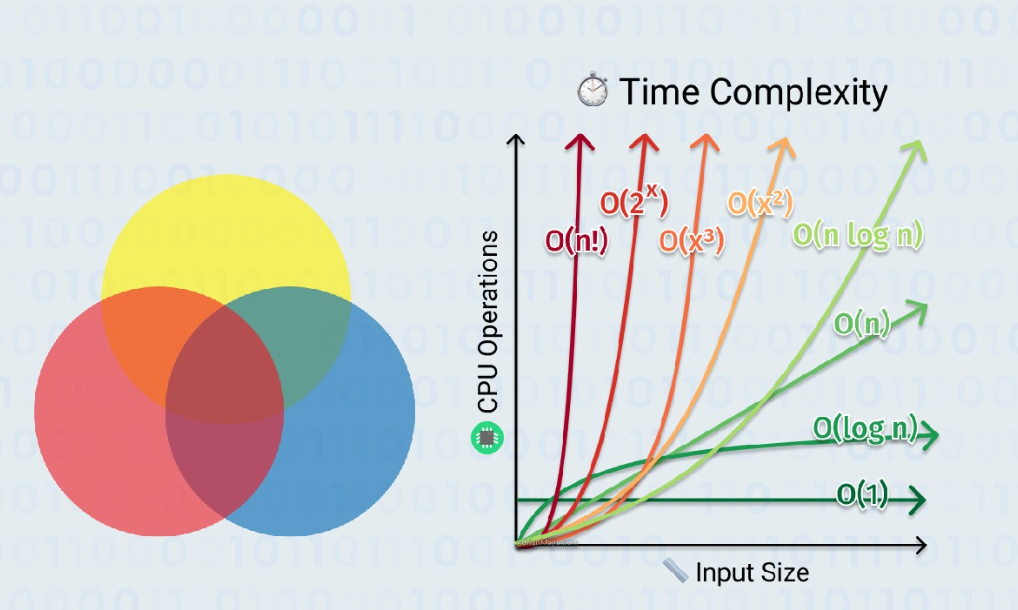
時間複雜度常以「大O符號」（O符號）來表示，表示最壞情況下的執行時間。以下列出幾種常見的時間複雜度：

• O(1)：常數時間複雜度，表示不管輸入的大小如何增加，算法的執行時間是恆定的。
• O(log n)：對數時間複雜度，常見於二分搜索等分而治之的演算法。
• O(n)：線性時間複雜度，表示執行時間與輸入大小成線性關係。
• O(n log n)：線性對數時間複雜度，常見於快速排序和合併排序等演算法。
• O(n^2)：平方時間複雜度，常見於嵌套迴圈等演算法。

舉例來說，如果一個算法的時間複雜度為O(n)，當輸入數據增加一倍時，執行時間也會增加一倍。

以下是一個簡單的Python範例，計算n個數字的總和：

1def calculate_sum(n):
2    total_sum = 0
3    for i in range(1, n+1):
4        total_sum += i
5    return total_sum
6
7n = 10
8result = calculate_sum(n)
9print("Sum of first", n, "numbers:", result)

在這個例子中，因為它包含一個for迴圈，迴圈的次數與n成正比，計算總和的循環執行了n次，因此時間複雜度為O(n)。

空間複雜度 Space Complexity

簡單的來說就是，電腦執行演算法所需要耗費的空間 ( 記憶體 ) 成本。

空間複雜度描述了算法執行所需的記憶體空間，也常以「大O符號」表示。與時間複雜度類似，空間複雜度也描述了最壞情況下的記憶體利用情況。

以下列出幾種常見的空間複雜度：

• O(1)：常數空間複雜度，表示算法使用的記憶體與輸入大小無關。
• O(n)：線性空間複雜度，表示空間利用與輸入大小成線性關係。
• O(n^2)：平方空間複雜度，表示空間利用與輸入大小的平方成正比。
• O(log n)：對數空間複雜度，常見於遞歸算法中的深度。

我們一樣以計算n個數字的總和為例：

1def calculate_sum(n):
2    return n * (n + 1) // 2
3
4n = 10
5result = calculate_sum(n)
6print("Sum of first", n, "numbers:", result)

這個算法的空間複雜度是O(1)，因為它只使用了一個變數來存儲總和，與輸入大小無關。

總結

時間複雜度和空間複雜度是評估演算法效率的重要工具，對於LeetCode解題也至關重要。我們應該充分了解這兩個概念，並在解題時考慮最優解，這將有助於我們在演算法的世界中取得更大的成就。

解釋完時間複雜度與空間複雜度後，那對於LeetCode刷題上會有什麼幫助呢？

在刷LeetCode時，有時光搞懂問題需求並轉換成程式語言就搞很久了，通常第一版效率都是最直觀的解法，而部分的LeetCode題目也要求我們考慮節省空間，尤其是在面對大數據集時。尋找具有較低空間複雜度的解決方案至關重要。